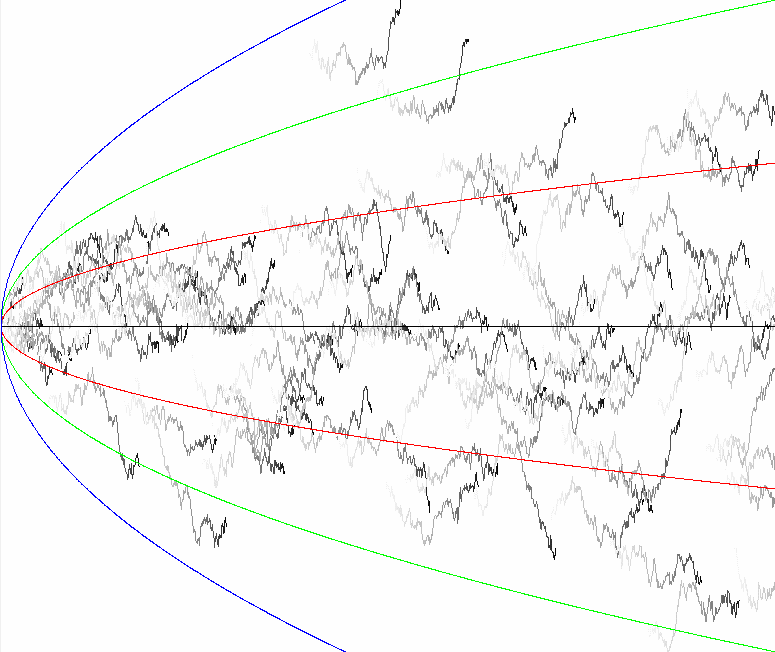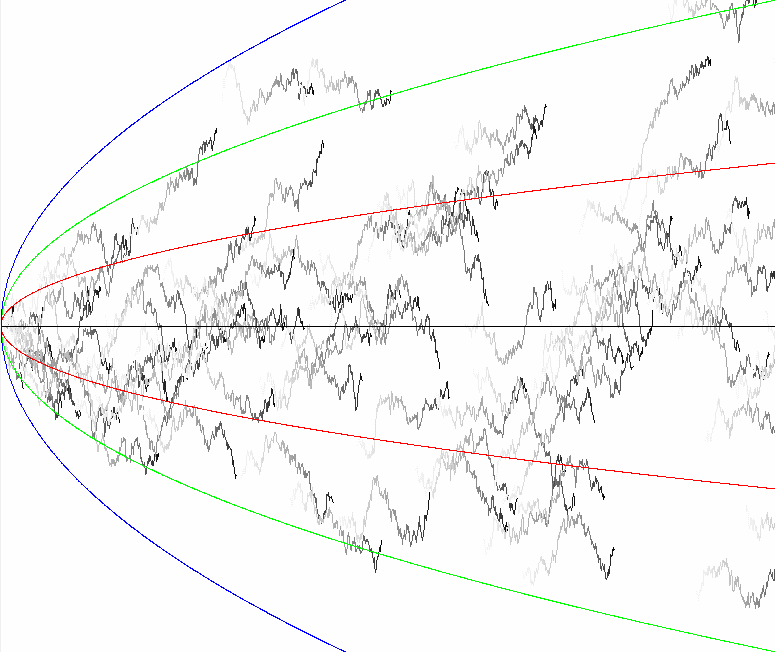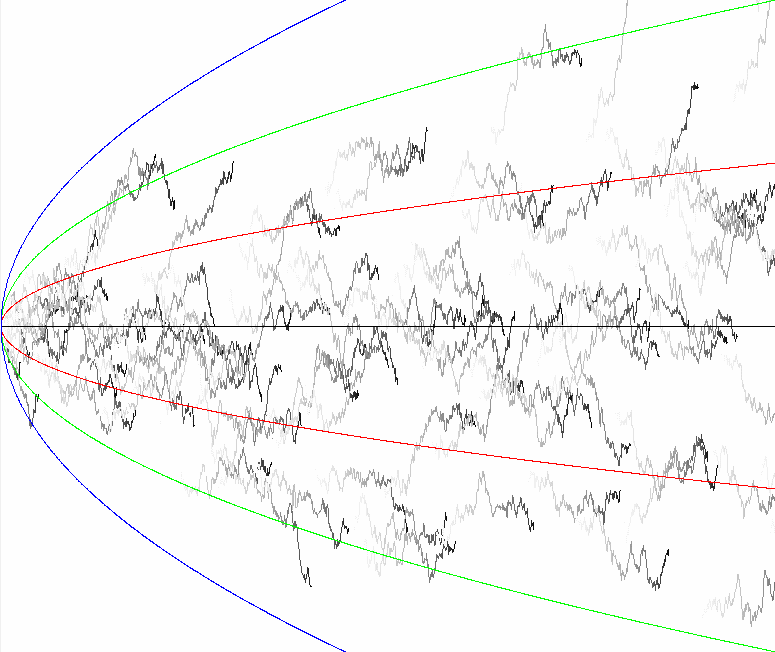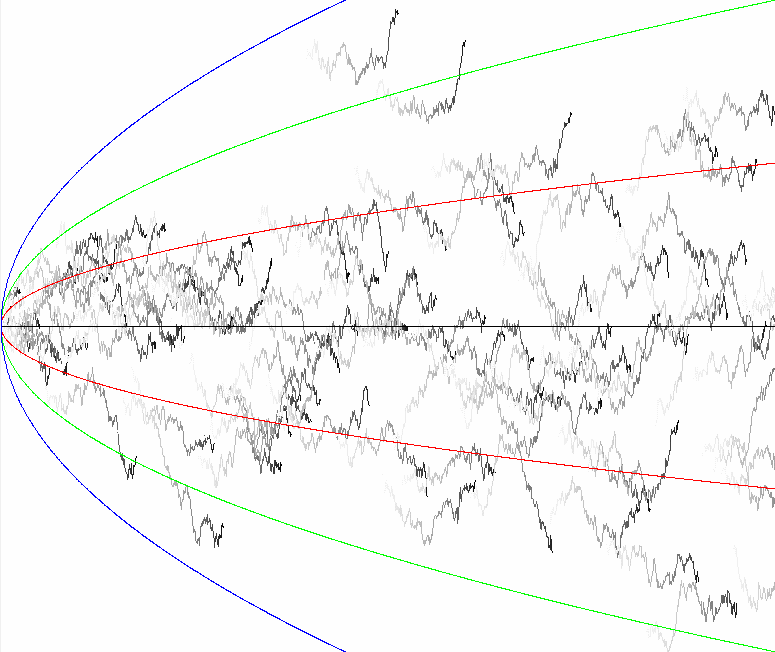
Stochastic Processes
In this blog post, we will delve into the fascinating realm of stochastic processes. We’ll begin with a concise yet informative introduction to stochastic processes. Subsequently, we’ll explore various properties, introduce crucial examples, and investigate their characteristics.
Introduction
First let us recall the definition of a random vari...

Local Variations in Functions
In this article, we delve into the intricacies of local variations in functions. We extend the concept of Lipschitz functions from univariate to multivariate functions and establish a connection with the operator norm of the Jacobian matrix. Additionally, we explore how different norms can yield diverse interpretations of Lipschitzness, offering...

Information geometry
Information geometry can be thought as part of the Information sciences which study the “communication” between data and families of models. In short, they seek to distill information from data to models. This includes information theory but also the fields of probability theory, statistics, machine learning and more. In contrast to these fields...
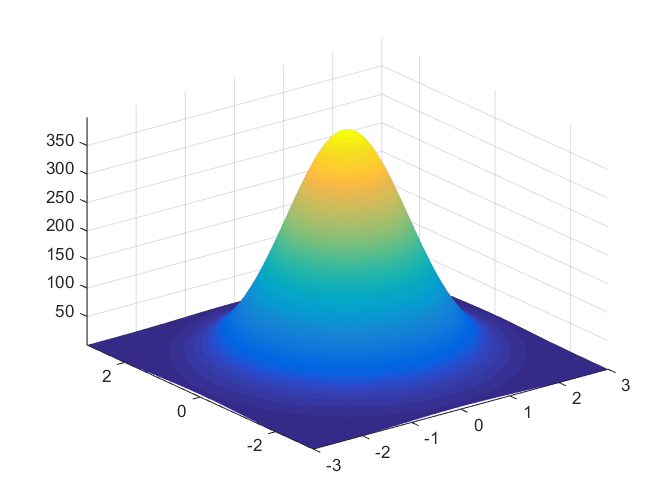
All about Fisher information
Fischer information plays a pivotal role in statistics; as we will see in some way or another, it will pop up in both Frequentist and Bayesian statistical paradigms. In this post, I will introduce the Fisher information together with some essential properties. We will review several applications and relationships of the Fischer information to ot...
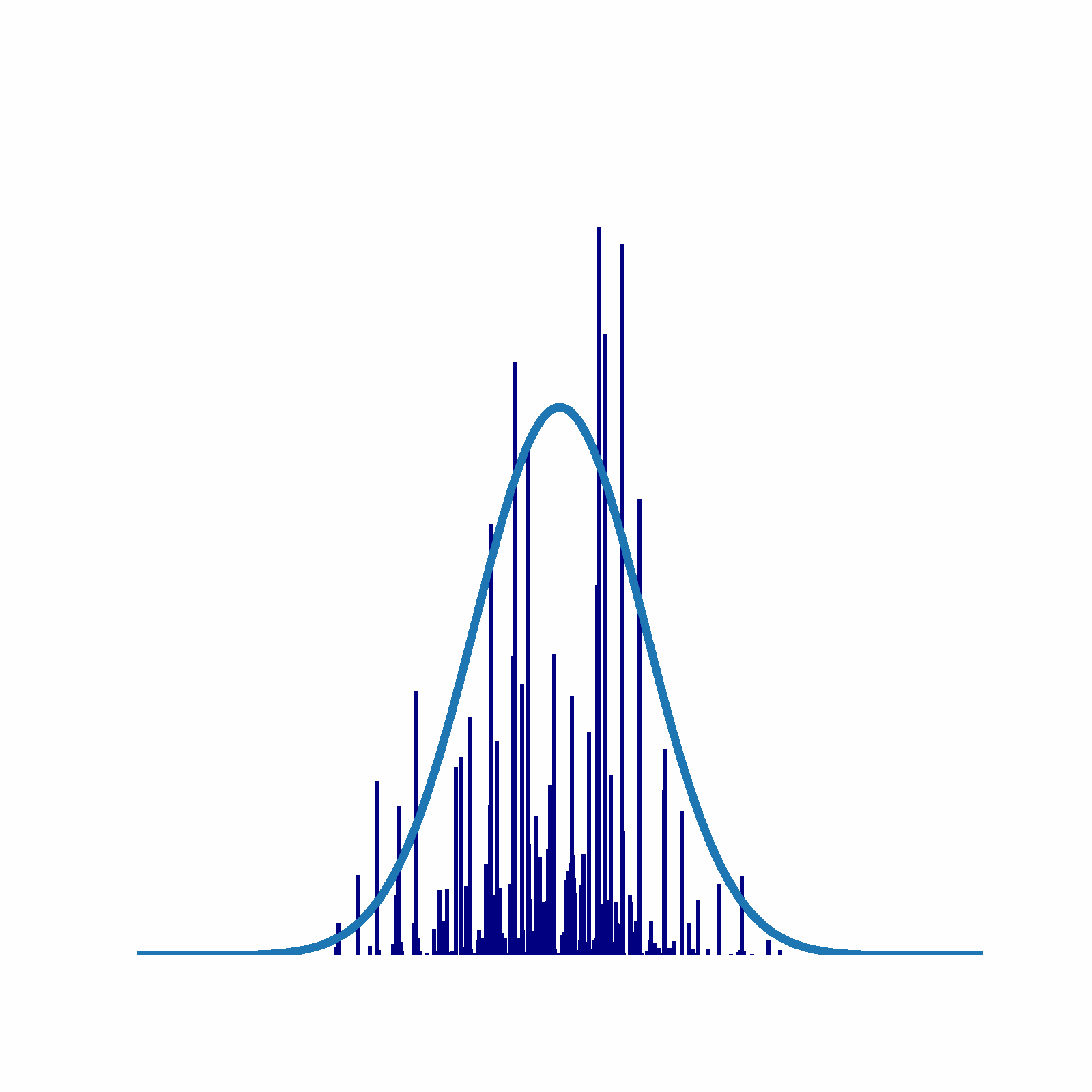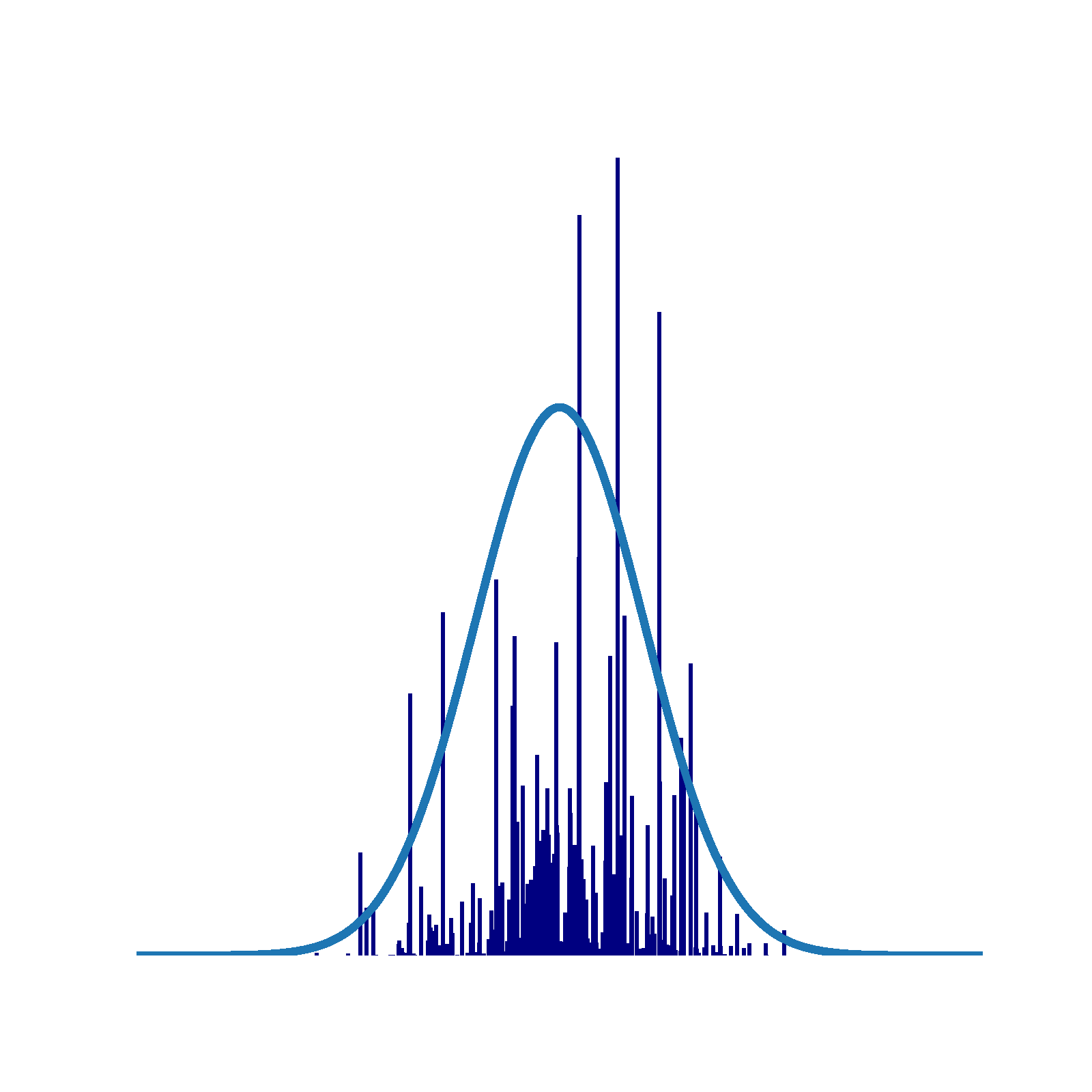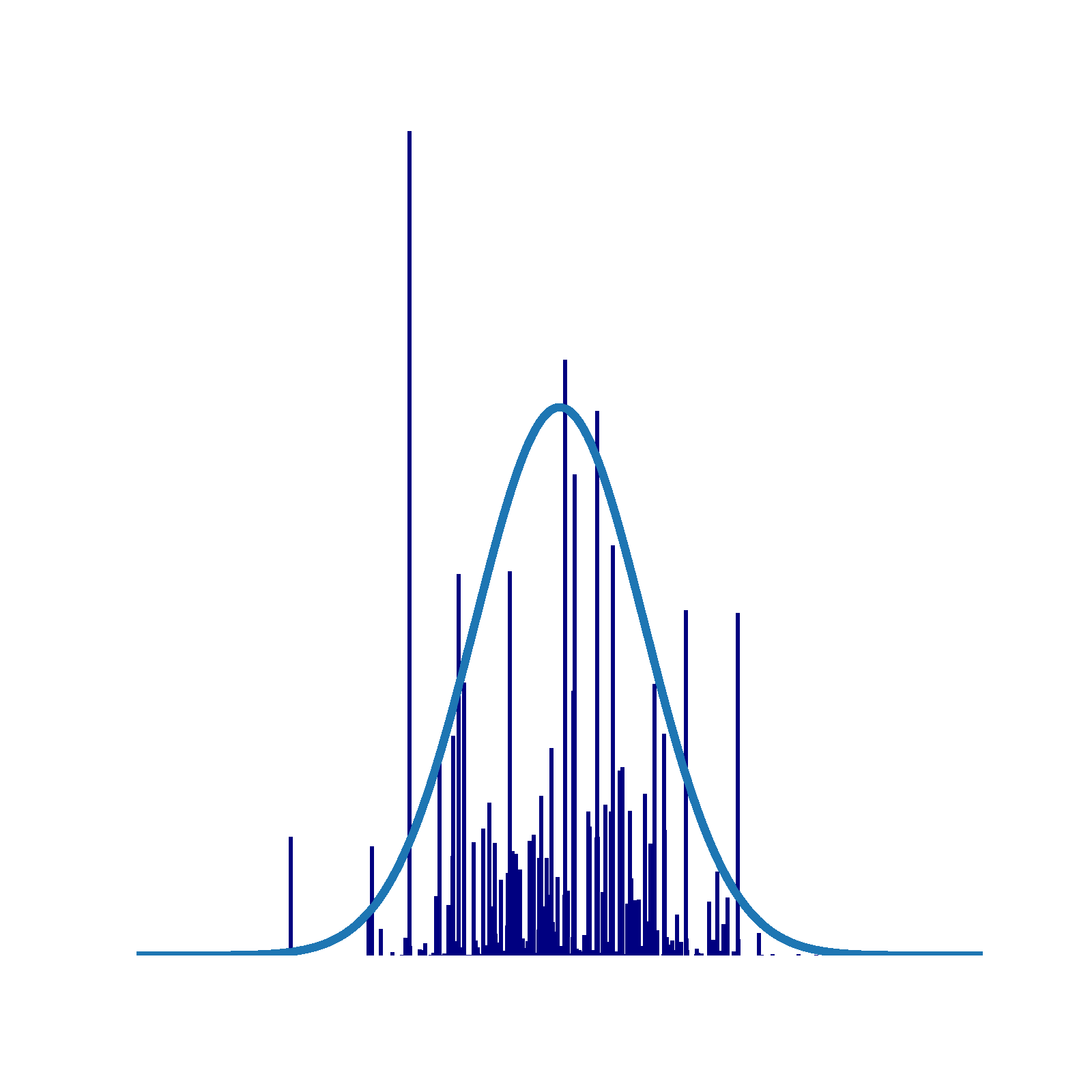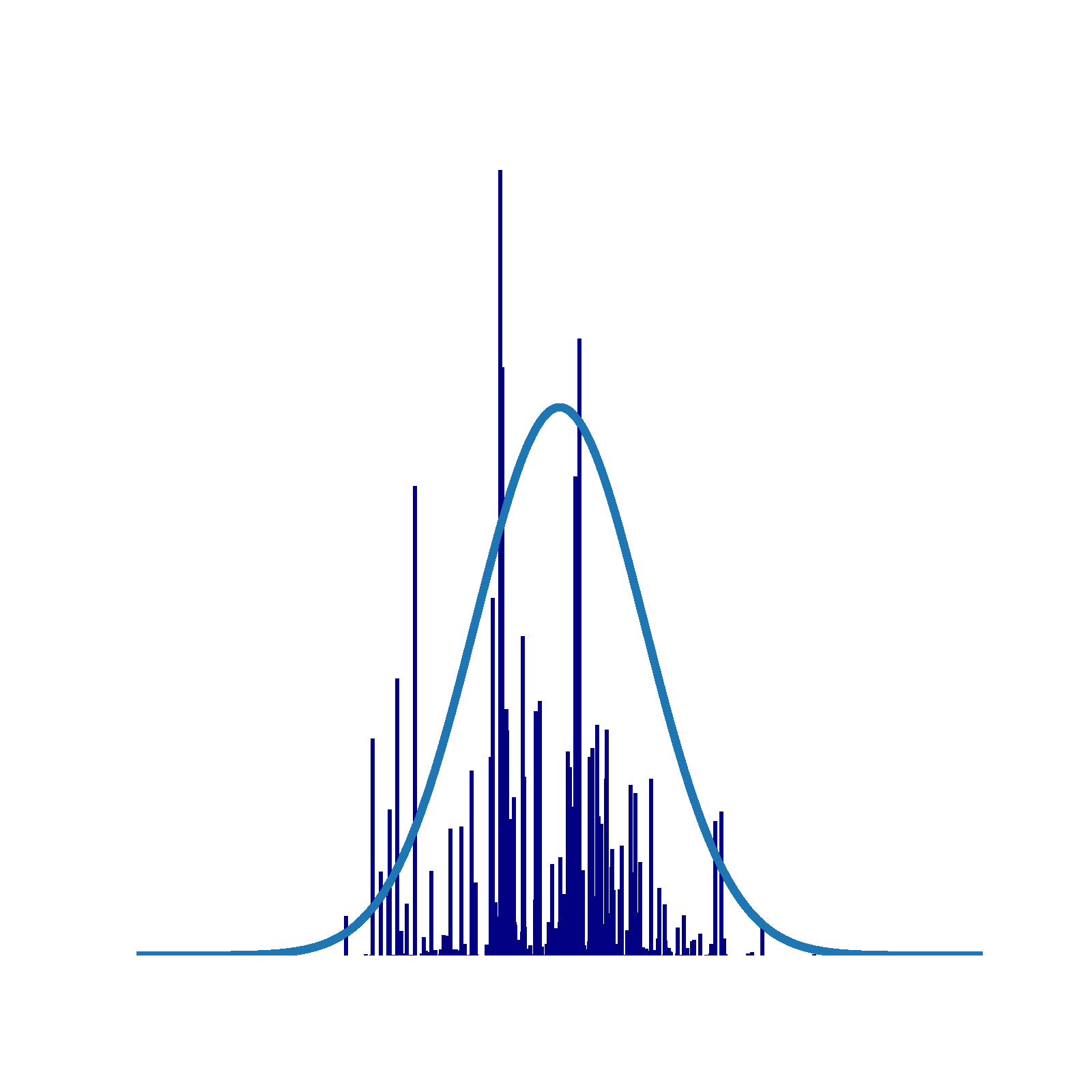
Bayesian Nonparametrics: An interactive guide
Traditional parametric models, characterized by a fixed and finite number of parameters, can encounter issues of data overfitting or underfitting when there is a mismatch between the model’s complexity (often represented by the parameter count), the complexity of the true data generation process, and the available data volume. Consequently, it f...

Welcome
Hey, welcome to this blog. Here I will post topics I care about and thinks I work on! 

 Here is a playground for cool techniques I use to write articles.
Theorems and Proofs
I created a nicely looking theorem, lemma, definition and proof classes.
[def]
A set $C$ is convex if for all
$x,y \in C$ and for all
$\alpha \in [...
Here is a playground for cool techniques I use to write articles.
Theorems and Proofs
I created a nicely looking theorem, lemma, definition and proof classes.
[def]
A set $C$ is convex if for all
$x,y \in C$ and for all
$\alpha \in [...